Obstacle Avoidance and Path Planning

Assumptions:

• The problem assumes the radius of the robot as 0.5 units.
• The obstacles are only rectangular in shape.
• The area is limited to 15 x 15 units (for visualization purposes).

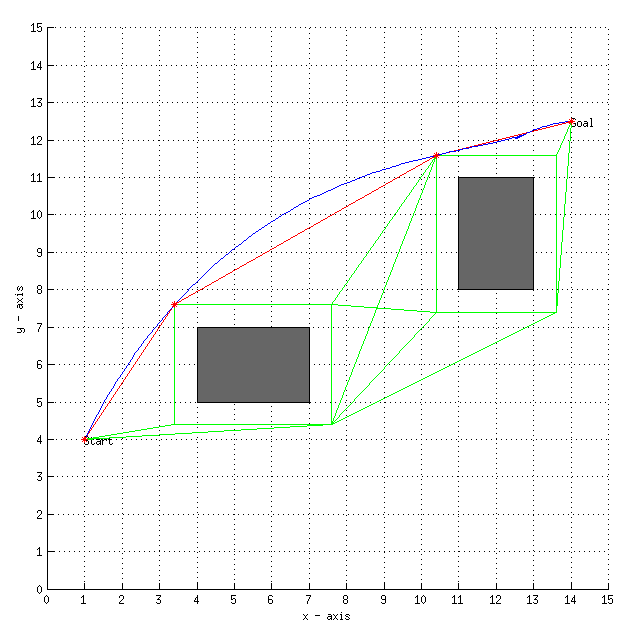
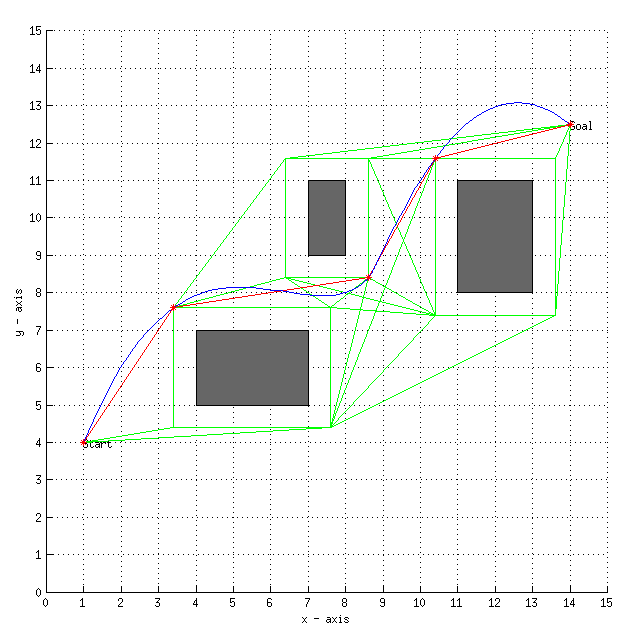
Reading the Plot:

• The solid filled rectangles represent the obstacles.
• The dotted lines around the obstacles represent the offset for the robot.
• The green lines represent edges of the visibility graph that were not finally selected.
• The red lines represent edges constituting the shortest path from start to goal.
• The start and goal points have been exclusively mentioned on the plot.
• The blue curve is the final path the robot will undertake.
• The points marked with ‘*’ are the intermediate points.

Approach:

• Initialization of start, goal, obstacles, offsets.
• Constructing an adjacency matrix
• Revising the adjacency matrix based on intersection with obstacle.
• Feeding the adjacency matrix to dijkstra(), implemented as a separate function.
• The output of dijkstra() is used to compute the Bernstein curve, as done in the last part of the project.
• The code is now generalized for maximum 3 intermediate points, order has been set constant at 5.
• The graph is plotted in sequence, and can be visualized as an animation.

Graphs related to 2 testcases are shown.